Richard Nakka's Experimental Rocketry Site
Richard Nakka's Experimental Rocketry Web Site
Derivation of equation describing chamber pressure due to igniter charge

From the ideal gas law, pressure within the chamber may be expressed as

Introducing the term G relating the fraction of igniter charge burned at any time t, and considering that the initial chamber pressure is ambient
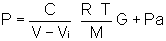
letting  ("effective force") gives
("effective force") gives
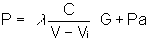
which may be rewritten as
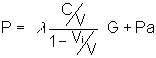
letting  (loading fraction) gives
(loading fraction) gives

multiply numerator and denominator by r (charge density)

since  , this gives
, this gives
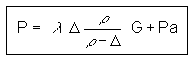
where:
P = pressure in combustion chamber at time, t lbf/in2
r= density of charge material lbm/in3
D = loading density = C / V lbm/in3 C = original mass of charge lbm
V = free volume of combustion chamber at time, t in3
l = R T/ M "effective force" (energy), in-lbf /lbm
R = universal gas constant in-lbf /°
R-lbm
M = effective molecular weight of combustion products (system mass divided by number of moles of gas) lbm /
mole
T = adiabatic flame temperature °
R
G = fraction of original charge mass consumed by time, t dimensionless
Pa = atmospheric pressure lbf/in2
Note that the assumption is made that combustion of the igniter charge occurs rapidly with no pressure loss due to gas seepage through the nozzle opening.
Back |


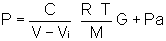
 ("effective force") gives
("effective force") gives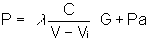
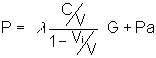
 (loading fraction) gives
(loading fraction) gives

 , this gives
, this gives