
The important physical properties of the fluid which affect the convection coefficient are thermal conductivity, viscosity, density (proportional to pressure), and specific heat of the fluid. Other parameters that affect the coefficient are the fluid velocity, geometry of the bounding surface, and pressure (to which fluid density is directly proportional).
In order to estimate this coefficient for conditions within a rocket motor, the casing may be considered to be a smooth tube with conditions of turbulent internal flow, with the following expression being applicable:

This equation is valid for
In these two equations, v, Di, Cp, m, r and k are the fluid velocity, tube diameter, fluid heat capacity, fluid dynamic viscosity, fluid density and thermal conductivity of the fluid, respectively. These fluid properties are all a function of temperature, but only density varies with pressure.
Physically, the Reynolds number may be considered to be a ratio of fluid inertia forces to viscous forces. The Prandtl number is the ratio of momentum diffusivity to thermal diffusivity, where diffusivity is the ability to facilitate heat transfer.
An alternative equation, more readily applied to rocket motor analysis, is
 (Ref. Mark's Hdbk. for Mechanical Engineers, 8th ed.)
(Ref. Mark's Hdbk. for Mechanical Engineers, 8th ed.)where C is a coefficient, with a value dependant upon whether English units or S.I. units are used in the equation
C = 0.024 (English units shown)
C = 3.075 (S.I. units shown), and where

The units of h are BTU/hr-ft2-F or W/m2-K.
Example:
Estimate the convection coefficient for a rocket motor powered by 1.50 kg. of 65/35 KN-Sorbitol propellant and a burn time of 1.1 seconds. Casing chamber dimensions are are 65 mm diameter by 400 mm length. The propellant grain is free-standing (unrestricted burning).
From Technical Notepad # 3, Cp' = 69.41 J/mol-K at the combustion temperature of 1600 K. From the same reference, the molecular weight of the combustion mixture is given as MW = 39.86 g/mol. Therefore
Cp = 69.41/39.86 = 1.74 J/g-K.
The average mass flow rate is w = 1.50/ 1.1 = 1.36 kg/sec., and the chamber cross-section area is S = p / 4 (65/1000)2 = 0.0033 m2 , giving the mass velocity
G = 1.36/ 0.0033 = 410 kg/sec-m2
This gives a convection coefficient of
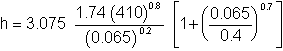 = 1457 W/m2-K.
= 1457 W/m2-K.