

Two-phase FlowMost solid rocket propellants produce combustion products that are a mixture of gases and condensed-phase particles (either liquid or solid) which is evident as visible smoke in the exhaust plume. Those propellants containing metals, such as aluminum or magnesium, generate oxides of the metals as condensed-phase combustion products. Metallic-compound oxidizers, such as potassium nitrate (KN) or potassium perchlorate (KP), generate condensed-phase products of particularly high molecular weight, which is rather undesirable. The KN-Sugar propellants produce a dense white cloud of potassium carbonate smoke. In fact, approximately 44% of the exhaust mass is solid matter! The occurrence of solids or liquids in the exhaust leads to a reduction in performance for a number of reasons:
In terms of the rocket performance parameters, the presence of condensed-phase products is reflected in a reduced Characteristic Velocity, due to the higher effective molecular weight of the gas/particle mixture. 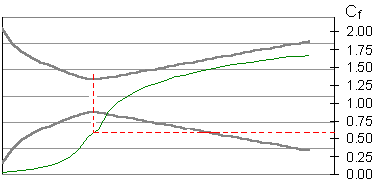 Another factor that is important with regard to two-phase flow losses is the nozzle contour, especially at the throat region. Figure 4 illustrates the flow acceleration for the Kappa nozzle. The acceleration in the region of the throat (red dashed line) is extremely high, especially just aft, where it is maximum. Most of the particle lag, which is a strong function of acceleration, occurs in this region, thus the importance of designing a nozzle with a well-rounded contour at the throat, without any sharp changes in cross-section.  The size of the rocket motor as well as condensed-phase particle size both play an important role with regard to the influence of two-phase flow effects. This is illustrated in Figure 5, which plots the fraction of Characteristic Velocity loss with respect to:
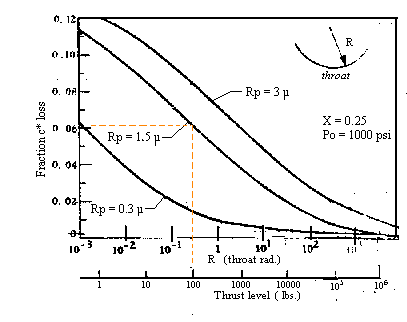 Ref. Dynamics of Two-Phase Flow in Rocket Nozzles, ARS Journal, Dec.1962
For example, for a 100 lb. thrust motor, the motor suffers a 6% loss in Characteristic Velocity if the average particle size is 1.5 micron, as shown by the red dashed line. How is two-phase flow taken into account with regard to motor performance calculations, such as those presented in the preceding Theory Pages? I asked myself that very question when I began researching the KN-Sucrose propellant from a theoretical performance aspect, back in 1983 when I began work on my B.Sc. thesis Solid Propellant Rocket Motor Design and Testing. All the equations in Sutton and other textbooks seemed to ignore the existence of particles in the exhaust, but I knew that I could not ignore this, not when the propellant exhaust contains 44% solid matter! After much consternation, I eventually managed to find a couple of books, and in particular, ARS Journal articles, that touched on this topic. I ended up re-deriving all the pertinent performance equations from basic principles, then made the necessary modifications to account for the presence of condensed-phase. A key assumption required was that the particles flow at the same velocity as the gas (i.e. no velocity lag), so the modified equations represent an upper limit on performance. The details are too involved to present here, so I will only present the final outcome, which fortunately, is quite simple. As it turns out, the gas-particle mixture behaves like a gas with a modified isentropic exponent, k. All the fundamental equations remain the same and are fully applicable to two-phase flow, with the only modifications being:
The derivation of this form of modified (two-phase) isentropic exponent assumes a frozen flow condition where no thermal or velocity particle lag is assumed to exist, and is based on the momentum and energy equations for steady isentropic flow. This is the form of k to be used, therefore, when calculating Exhaust velocity, Thrust, Thrust Coefficient and the other nozzle flow parameters. Additional details on the calculation of this modified isentropic exponent may be found in the Technical Notepad Web Page and in the ARS Journal article "Recent Advances in Gas-Particle Nozzle Flows", R.F. Hoglund, May 1962. This equation for the two-phase isentropic exponent is used in the NASA computer code "AXISYMMETRIC TWO-PHASE PERFECT GAS PERFORMANCE" (MSC-11774). For those interested in more of the theoretical treatment of two-phase flow, I'd suggest perusing Solid Propellant Rocket Motor Design and Testing which is available for downloading in PDF format. Also see Isentropic exponent modified for 2-phase flow, alternate expression |
